产品分析之统计学悖论

在做产品分析时，统计结果截然相反，是何种原因引起的呢？这种情况该如何应对呢？

近期面试聊到了产品分析时统计结果截然相反时，分析人员变成了热锅上的蚂蚁，手足无措。这到底是什么引起的呢？早在1951年性别歧视的案子中就发现了这种相悖的统计结果。

最典型的例子: 1973年加利福尼亚大学伯克利分校性别歧视案的例子：

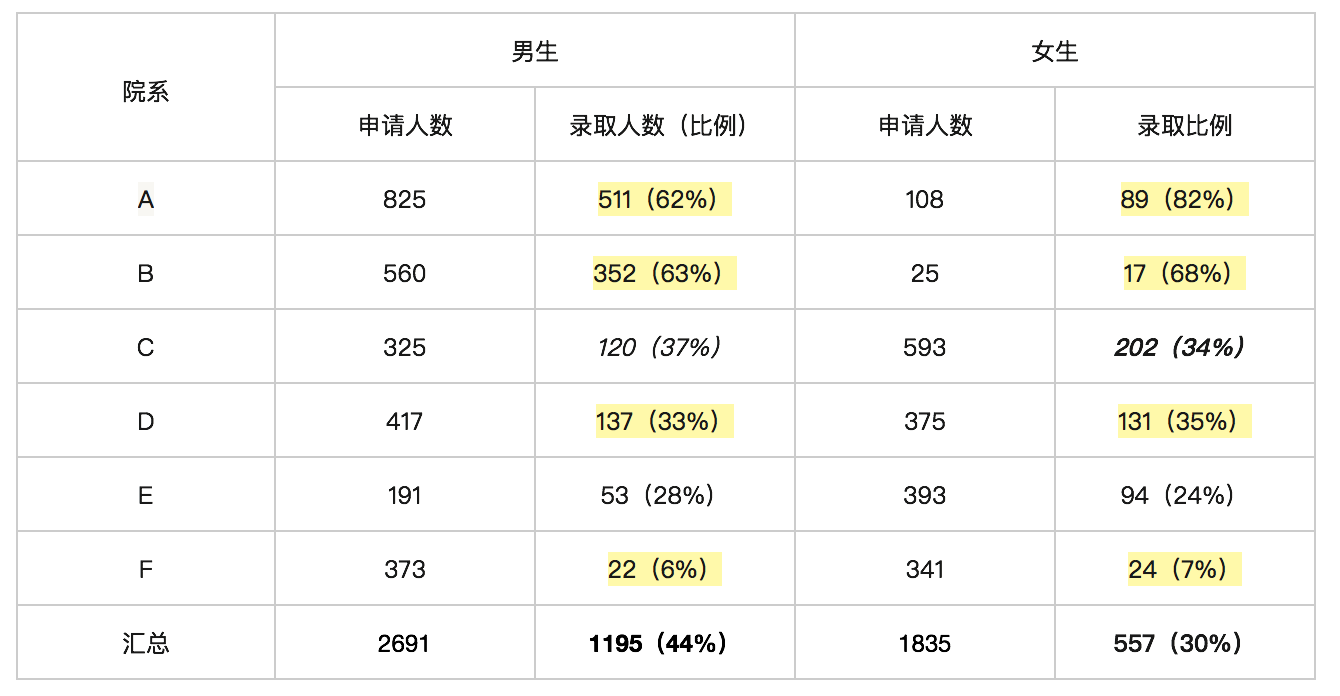
大家从表格里可以看到，如果只看整体录取率，那么男生的录取率是44%，女生的是30%。

但加利福尼亚大学伯克利分校的统计学教授 Peter Bickel 后来发现，如果按照院系分类，女生实际上比男生的录取率还高一些。

一、细节和整体趋势完全不同

辛普森悖论（Simpson’s paradox）：当你把数据拆开细看的时候，细节和整体趋势完全不同的现象。

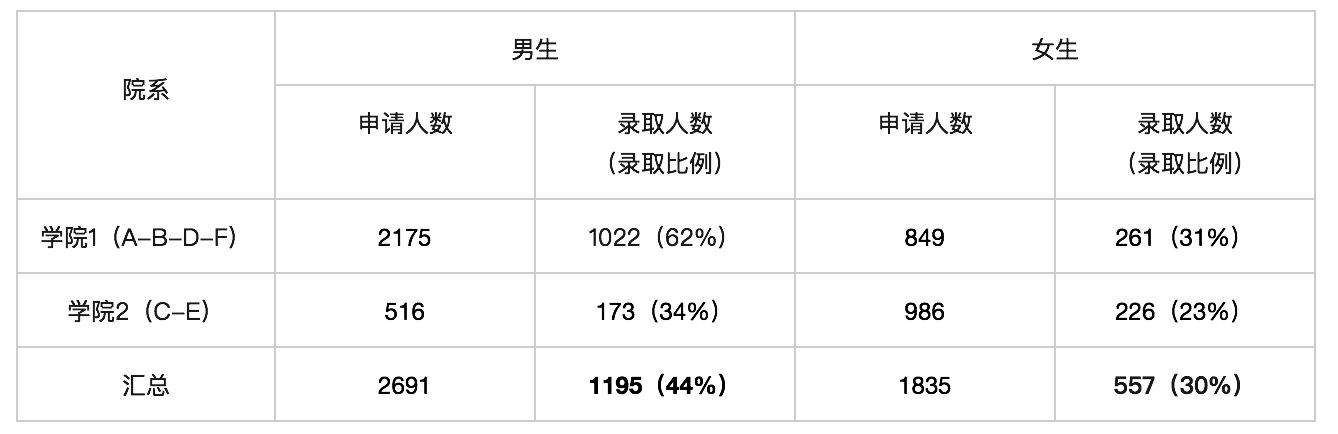
我们简化上述表格，发现悖论是由于基数产生的影响——男生在学院1和学院2的分布和女生的分布截然相反引起的。

在日常分析工作也经常存在这样的现象，经常在两端分析时，大都以为两端作为拆分对比，如iOS、Android投放广告的转化率分析中，通过两端的转化率可以得到结论1，但将iOS、Android按照网页版本、移动版本拆分后会得到完全相反的结论：

结论1: iOS的总体转化率低于Android。

基于此可以得到的结论是该批次广告不适合iOS平台；

iOS平台需要做在转化过程中需要做进一步的漏斗分析以便优化。

结论2: 网页版本iOS的转换率高于Android，且移动端iOS的 转化率也高于Android。

基于此可以得到的结论是该批次广告不适合Android平台；

Android平台需要做在转化过程中需要做进一步的漏斗分析以便优化。

如果没有辩证的结合多个维度分析该数据表现，则会被误导，在错误的方向上投入更多的精力，甚至是完全相反的决策。

二、相关分析中，整体相关性和组间相关性相反。

假设我们有每周运动小时属于两组患者（50岁以下、50岁以上的患者）患病风险的对比数据。以下为两组患者患病可能性的散点图：

由下图（x轴是运动小时数、y轴是风险）可以得到的结论是：患病风险与运动小时数呈负相关。

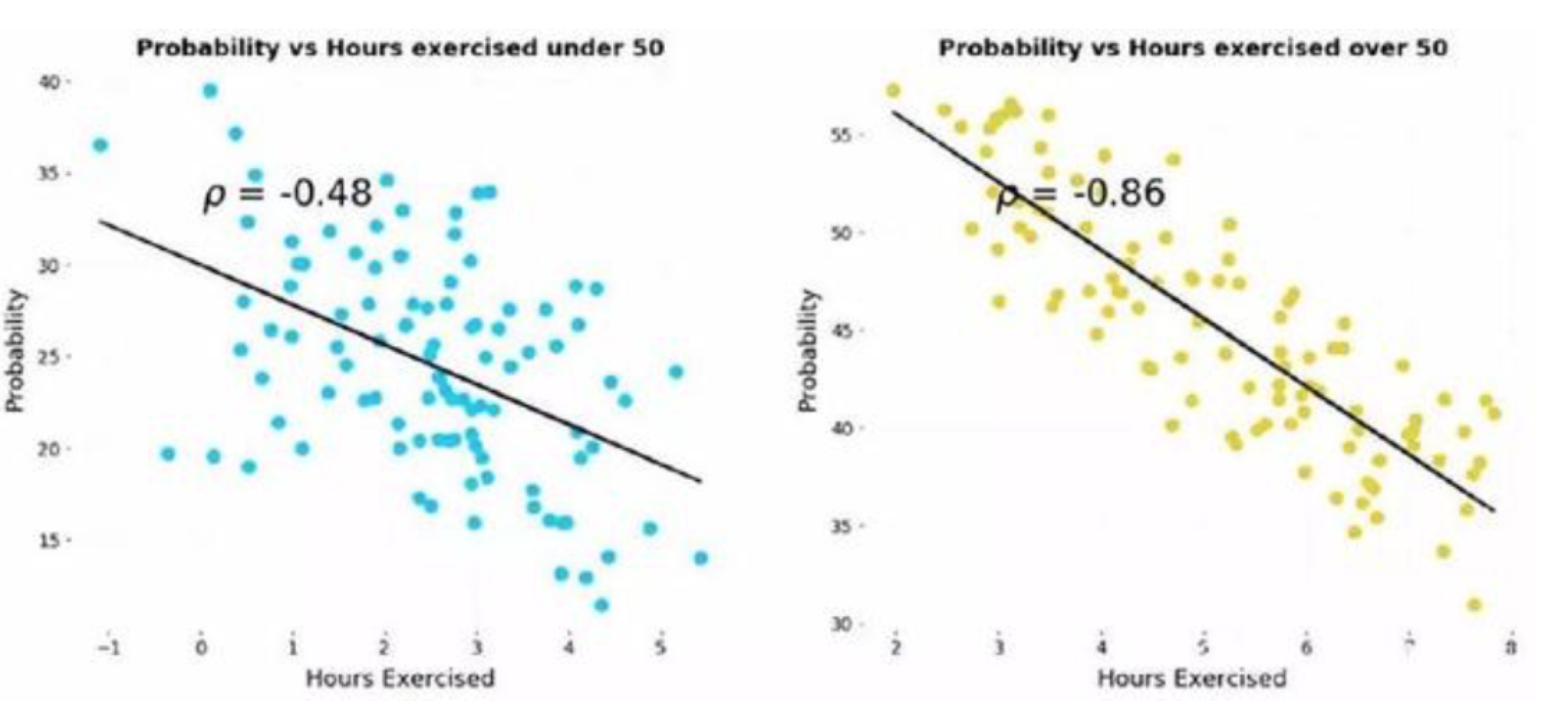
将2组数据合并后，得到的结论是：患病风险与运动小时数呈正相关。与分组结论皆然相反。

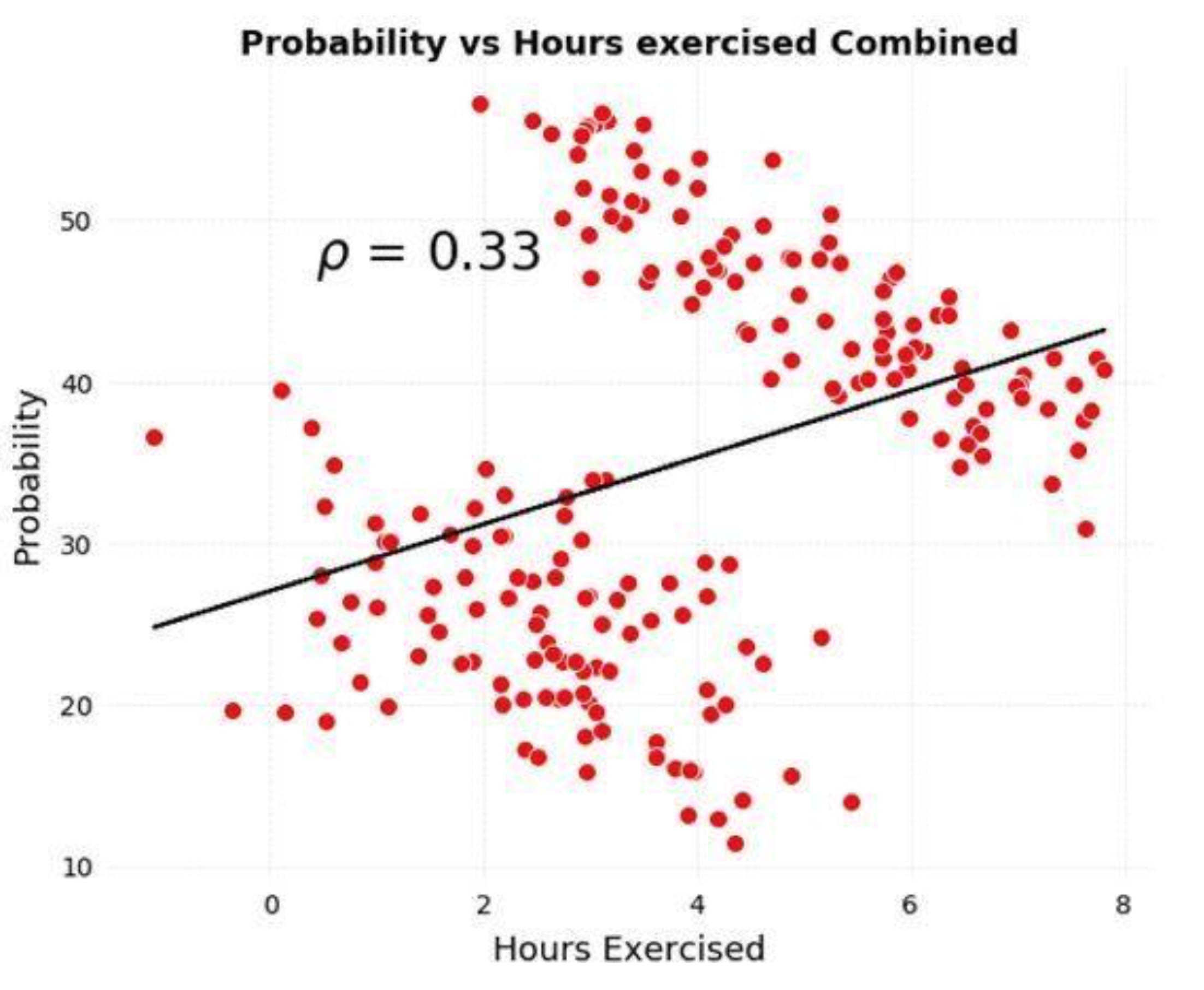
原因是：患病几率是由多种因素引起的，年龄比运动时间的影响程度更大。在分析运动时间与发病几率时，忽略了年龄等其他因素——而进一步拆分后，会得到完全不同的结论。

先前恰巧有通过相关性分析来探讨变量与留存、回访间的关系。

不同停留时长的用户在留存上面的表现，发现停留时长越长的用户留存以及回访现象越不好，这和app使用基本认知相反；

而结合用户用户行为深度分析发现，用户行为越深留存以及回访现象越好。相比笼统的停留时长（包括app使用时长、后台时长），用户行为深度对用户留存以及回访影响更大，其相关表现也更符合真实的现象。

数据分析相比数据挖掘、深度学习，最大的优势就是可解释性，得到的结论需要多结合场景、用户属性思考，是否看到了数据的全貌。

三、AB测试中细分结果和整体结果相悖

AB测试中细分结果和整体结果相悖则要小心了……来看下面这个例子：

通过A、B两种疗法结石的治愈率来看哪一种疗法更好。

基于大结石、小结石，A疗法都比B疗法要好；但汇总结果却是B疗法比A疗法要好。无法判断那个疗法更好。

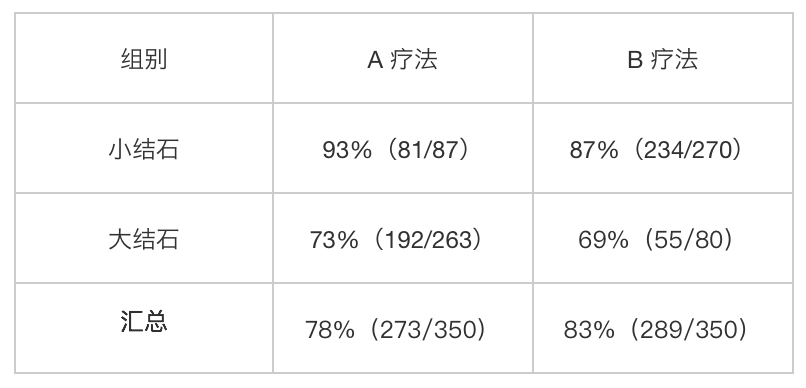
你应该看了本文的第一个例子，可以发现A、B疗法在不同类型的结石中基数差异引起了问题。

在两个组内不同类型的结石中基数差异可能是由第三中因素引起的，如该例子因为医生似乎觉得病情较重的患者更适合 A 疗法，病情较轻的患者更适合 B 疗法，所以下意识的在随机分配患者的时候，让 A 组里面大结石病历要多，而 B 组里面小结石病历要多。