如何利用囚徒困境，让选择的利益最大化？

1. 精英律师

又是岁末年初。

南方的城市里，虽未至严冬，已颇有寒意，正是三两知己一边火锅一边畅谈的相聚好时机。

青子看着电视里正在放着的《精英律师》，说道：

“这集看过了，说的是富豪百亿遗产争夺案，富豪弟弟和富豪老婆，争来争去，到最后选了个和解方案，谁也没有成功独吞全部财产。”

【精英律师-剧照】

未待众人接话，青子像是突然想起了什么，对着唐寂大声说道：“有利有弊，互相猜忌，最后两边折衷和解，这是不是你以前跟我讲的那个什么…..什么罪犯案例？”

唐寂看了一眼电视，答道：“是囚徒困境。”

2. 囚徒困境 2.1“囚徒困境”理论简介

囚徒困境（Prisoner’s Dilemma），是博弈论的非零和博弈中极具代表性的例子。

非零和博弈是指博弈中各方的收益或者损失的总和不是零，区别于零和博弈（例如“你”赢就一定“我”输的对赌），是一种合作下的博弈。

囚徒困境指出，个人的最佳选择可能并非团体最佳选择，或者说，在一个群体中，个人做出理性选择（个人利益最大化）时，却可能导致集体的非理性（集体利益非最大化，甚至集体利益最小化）。

囚徒困境的故事，可简述为：

警方逮捕了甲、乙两名嫌犯，但并没有足够证据指控二人入罪。于是，警方分开囚禁甲、乙，并分别和二人见面，且向双方提供以下相同选择：

若一人认罪并作证检举对方，而对方保持沉默，则此人即时无罪获释，沉默者判刑10年；

若二人皆沉默不检举，则二人同时判刑1年；

若二人相互检举，则二人同时判刑7年。

最终，甲乙二人在以下合理前提条件下：

被隔断无交流

均获知惩罚的确实有效性

确认抉择后对方无报复手段

双方皆为理性人，会最大限度为自己争取利益

最终选择“相互检举”，导致”二人同时判刑7年”。

2.2《精英律师》案例分析

在《精英律师》案例中，富豪孙浩瀚留下了百亿遗产，孙超越（孙浩瀚亲弟）与蓝红（孙浩瀚妻子）针对继承权问题对簿公堂。

围绕是否存在合法有效的遗嘱，双方面临的情况是：

若存在合法有效的遗嘱，孙超越为合法继承人；

若不存在合法有效的遗嘱，蓝红作为配偶，是法定继承人。

因此，在诉讼与和解的抉择面前，二人的博弈是：

但最终，二人没有走到“让对方零继承”的最坏局面。

通过双方律师和当事人的正确判断与有效博弈，在基于“孙浩瀚既不希望亲弟零继承，也不希望妻子零继承”的情理之上，二人最终达成“相互体谅”的和解。

【精英律师-剧照，来源：爱奇艺】

“百亿家产啊，如果是我，我就赌一局！”

“那我可提醒你，相比于翻倍叫地主，这刺激程度可能更接近于俄罗斯轮盘赌。”

“按50-50的概率算，理论上的数学期望，应该跟和解方案相近。”

“哈哈，那还是不要赌这一局了。”

“还有类似的案例吗？”

“再给你说个候选人投票的故事吧。”

3. 三中选一

候选人投票故事：

现有甲乙丙评委三人，需对ABC候选三人进行投票，投票规则如下：

评委每人对ABC三人进行排序，排序一二三分别对应计分3、2、1；

三位评委的排序投票求和，总计分最高者，胜出；

如三位评委的投票排序皆为ABC，则A计9分，B计6分，C计3分，A胜出。

已知以下情况：甲欣赏A，乙欣赏B，丙态度不明。

请问：甲是否存在一种策略，最大概率使A胜出？

……

“既然甲想选A，A得3分，乙想选B，B也得3分，那关键就是丙想选谁，因为丙的第一顺位也是3分。”

“那也不一定，排第二也有2分，两个2分，跟一个3分一个1分，都是4分。”

“对啊，你也说了，问题就在于只有三个人进行321排序，只要拿到一个3分，另一个至少有一个1分，那也是立于不败之地了。”

“问题是没说丙一定会给A投3分啊？”

“那这个问题，是不是可以先讨论到底需要多少分才能保证不被淘汰！”

“在数学上，这确实是排列组合的概率和期望问题。”

3.1 囚徒困境下的概率问题

先回到上面《精英律师》里的案例，若假设有：

遗嘱有效的的概率为50%；

诉讼胜利获得全部遗产，100亿；

诉讼失败则零继承，0收益。

那么，蓝红和孙超越在博弈中的数学期望，应该是：

E=100*0.5+0*（1-0.5）=50（亿）

因此，折衷和解，于情于理，符合双方预期利益。

再看“三选一”案例，其数学本质更接近于如下条件中的排列组合问题。

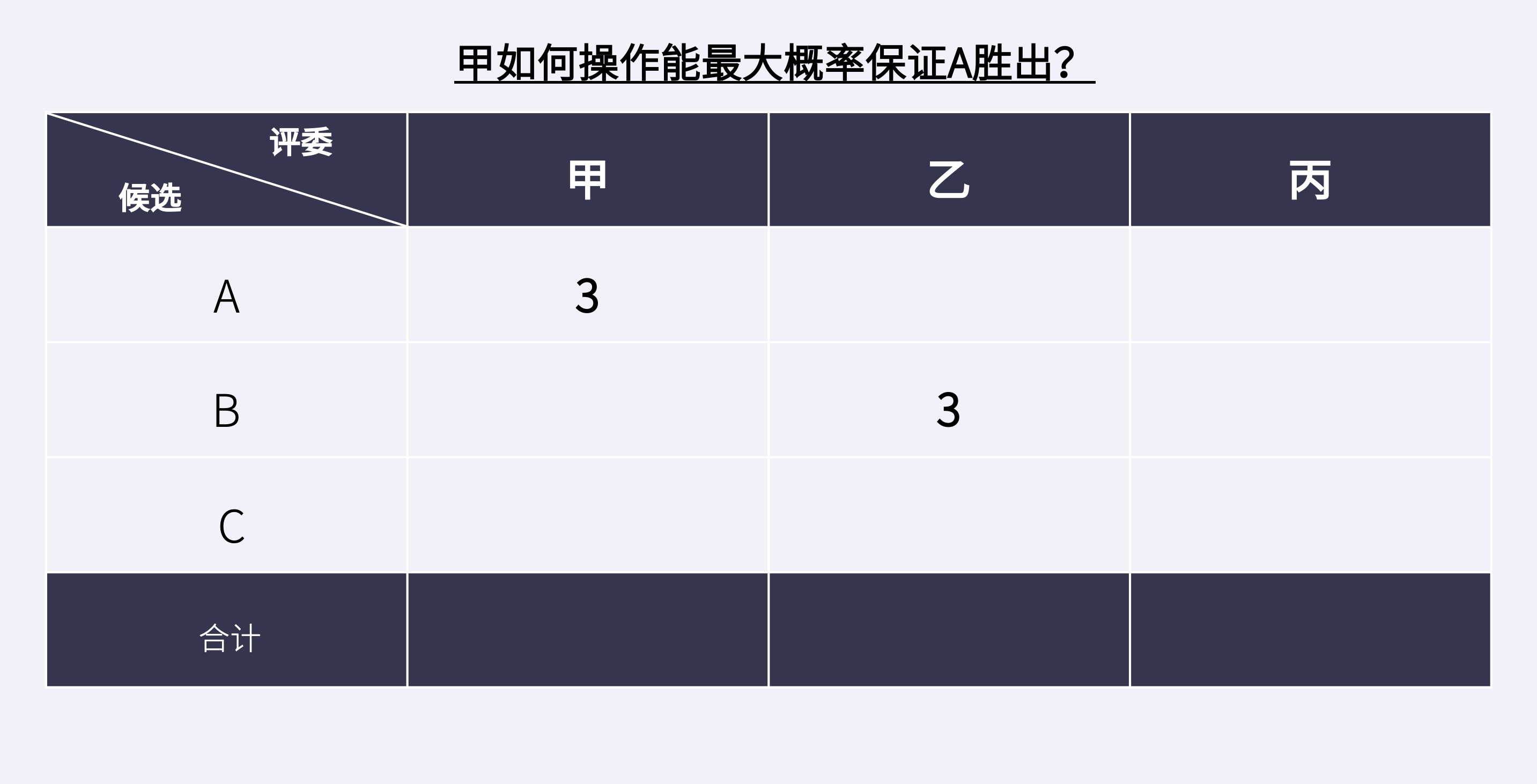
假设有：甲已将3分赋予A，乙已将3分赋予B

则请问：甲将2分赋予给B和C中的哪位，可使得A得到最多分的概率最大？

本文不展开探讨具体的概率计算问题，感兴趣的读者，可以留言探讨——A需要至少得多少分，才能保证胜出？

3.2 囚徒困境下的博弈问题